بله چنین تابعی تابع صفر است. برای اثبات نقطه ی دلخواه $ A $ در صفحه را در نظر می گیریم و نقاطی بصورت زیر را اختیار میکنیم که تمام چهار ضلعی ها مربع هستند.
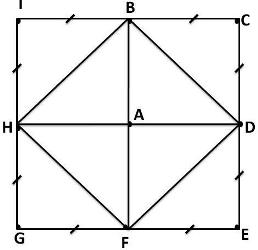
برای مربع های$ ICEG $ ، $ BDFA $ داریم:
$$ 1)f(C)+f(E)+f(G)+f(I)=0 $$
$$ 2)f(B)+f(D)+f(F)+f(H)=0 $$
حال کافیست برای مربع های $ HABI$ ، $ AHGF $ ، $ ADEF $ ، $ ABCD $$$ f(A)+f(B)+f(C)+f(D)=0 $$
$$ f(A)+f(D)+f(E)+f(F)=0 $$
$$ f(A)+f(F)+f(G)+f(H)=0 $$
$$ f(A)+f(H)+f(I)+f(B)=0 $$
با جمع طرفین و توجه به ستون ها و استفاده از روابط $1$ و$2$ بدست می آید که $4f(A)=0 $ لذا $f(A)=0 $ و چون نقطه دلخواه بود لذا $ f $ تابع صفر است