چگونه میتوان اثبات یا رد کرد که به ازای هر $x$ طبیعی ، در بازه $x^2 . . .\frac{3x^2+7}{2}$ حداقل تعداد اعداد اول، مساوی $x-1$ است؟ این مطلب را بصورت تجربی در جدول تفاضل مربعات مشاهده کردم که قادر به اثبات یا رد آن نیستم. عکس جدول خود را به پیوست ارسال میکنم. نکته جالب در این جدول وجود اعداد نیمه اول (semiprime) هایلایت شده در زیر هر ستون و افق هر ردیف است که با این مطلب و احتمالاً به حدس گلدباخ نیز مرتبط است. استادان عزیز حتماً توجه دارند که برای اثبات حدس گلدباخ باید ثابت شود اعداد بالای جدول از $4$ به بعد نقطه تقارن دو عدد اول است که با جمع آنها $2x$ بدست می آید و با ضرب آن دو عدد اول، عدد نیمه اول زیر ستون $x$ بصورت هایلایت قرار میگیرد. با توجه به اینکه اعداد زیر هر ستون $x$ بصورت
$(x-a)(x+a)=x^2-a^2$
می باشد، اثبات طرح این سؤال شاید نشان دهد تعداد اشباع شده ای از اعداد اول در سمت راست $x$ تا $2x$ وجود دارد که با یکی از اعداد اول سمت چپ $x$ ، عدد نیمه اول تشکیل دهد و زیر ستون $x$ بصورت عدد نیمه اول هایلایت شده ظاهر شود و جمع آنها بصورت $2x$ نیز برآورده شود. صورت دیگر این مسئله که در جدول زیر قابل رؤیت است و نیاز به اثبات دارد این است که اگر $x>1$ باشد ، در بازه $x^2 . . . \frac{3x^2}{2} $ حداقل تعداد اعداد اول، مساوی $x-2$ است. چون این جدول با اکسل 2007 تهیه شده و ارسال خود جدول برایم میسر نبود، عکسی از آن ارسال کردم.
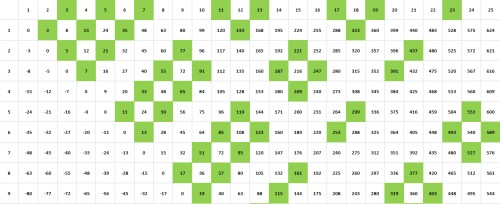
یکی از موضوعاتی که میتواند در کنار این مطلب کمک کننده باشد، وجود دستکم یک عدد اول در بازه ای بمراتب کوچکتر است که نتیجه ای از اصل برتراند است.
قضیه: بشرط $x \geq 48$ ، در بازه
$x . . . \frac{9x}{8} $
حداقل یک عدد اول وجود دارد.
نقل از کتاب
Prime Numbers_ The Most Mysterious Figures in Math
تألیف David Wells نشر Wiley سال $2005$ صفحه $21$
با قضیه فوق چندان سخت نخواهد بود ثابت شود که به ازای
$x > 1$
دستکم یک عدد اول در بازه $x . . . \frac{3x}{2} $
وجود دارد. امیدوارم مسئله گلدباخ سرانجام بدست توانای ریاضیدانان ایرانی حل شود.