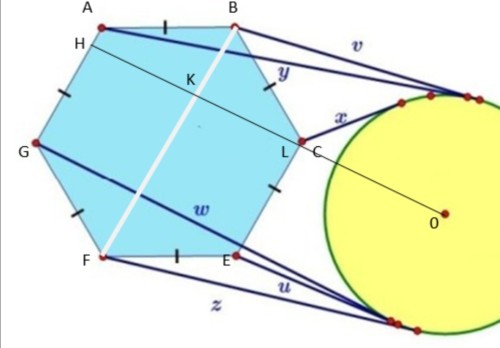
- متشابه راه حل مسئله در پست توضیحات لینک انجام می دهیم. مطابق شکل زیر از مرکز دایره بر یک ضلع (یا امتداد آن) عمود رسم می کنیم در نتیجه بر ضلع مقابل و یکی از قطرها عمود می شد.
می باشد با اضافه کردن
$3R^2 $
به طرفین تساوی خواهیم داشت
$$OC^2 +OA^2 +OF^2 =OB^2 +OD^2 +OG^2 $$
برای اثبات رابطه اخیر ابتدا نشان می دهیم سمت چپ مقدار ثابت است
$$OC^2 +OA^2 +OF^2=OL^2 +OK^2 +OH^2 +CL^2 +AH^2 +FK^2 \quad (1) $$
همچنین برای سمت راست هم داریم
$$O B^2 +OE^2 +OG^2=OL^2 +OK^2 +OH^2 +EL^2 +GH^2 +BK^2 \quad (2) $$
کافی است نشان دهید که رابطه زیر
$$CL^2 +AH^2 +FK^2=EL^2 +GH^2 +BK^2$$
درست است بنابراین از دو رابطه (1) و (2) نتیجه مورد نظر بدست می آید.
