ШЁЩҮ ЩҶШ§Щ… Ш®ШҜШ§
Ш¬Щ…Ш№ШҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶШҜ ЩҶШҙШ§ЩҶвҖҢШҜЩҮЩҶШҜЩҮЩ” Ъ©ЩҶШ§Шұ ЩҮЩ… ЩӮШұШ§Шұ ШҜШ§ШҜЩҶ ШҜЩҲ ШіШЁШҜ Ш§ЩӮЩ„Ш§Щ… ЩҲ ШҙЩ…Ш§ШұШҙ Ъ©Щ„ Ш§ЩӮЩ„Ш§Щ… ШЁШ§ШҙШҜ. Щ…ЩҮЩ… ЩҶЫҢШіШӘ Ъ©ЩҮ ШҙЩ…ШұШҜЩҶ ШұШ§ ШЁШ§ Ъ©ШҜШ§Щ… ШіШЁШҜ ШҙШұЩҲШ№ Щ…ЫҢвҖҢЪ©ЩҶЫҢШҜШҢ ШЁЩҮ ЩҮШұ ШӯШ§Щ„ШҢ ШЁШҜЫҢЩҮЫҢ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ ЩҮШұ ШӯШ§Щ„ШӘШҢ ШЁЩҮ ЫҢЪ© Ш№ШҜШҜ ЫҢЪ©ШіШ§ЩҶ Щ…ЫҢвҖҢШұШіЫҢШҜ. ЩҫШі ШЁЩҮ ЩҮЩ…ЫҢЩҶ ШҜЩ„ЫҢЩ„ШҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ЩҶШӘЫҢШ¬ЩҮ ЪҜШұЩҒШӘ Ъ©ЩҮ Ш№Щ…Щ„ Ш¬Щ…Ш№ШҢ Ш®Ш§ШөЫҢШӘ Ш¬Ш§ШЁЩҮвҖҢШ¬Ш§ЫҢЫҢ ШҜШ§ШұШҜ.
ШҜШұ Щ…ЩҲШұШҜ Ш¶ШұШЁШҢ Ш§ШЁШӘШҜШ§ Щ…ШіШӘШ·ЫҢЩ„ ШІЫҢШұ ШұШ§ ШҜШұ ЩҶШёШұ ШЁЪҜЫҢШұЫҢШҜ:
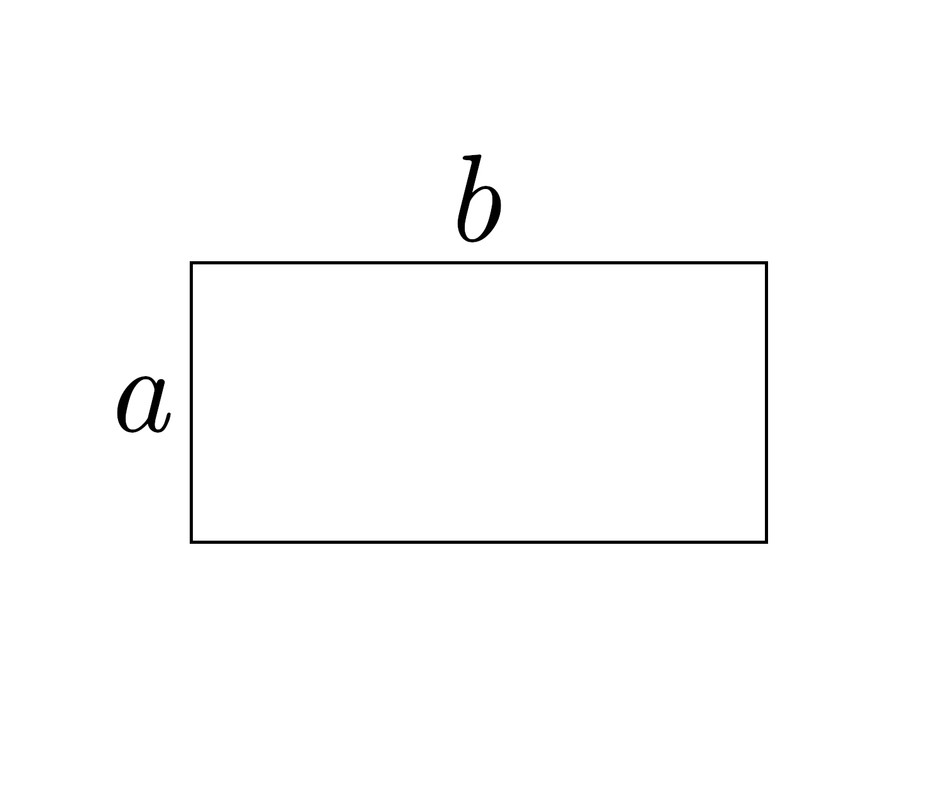
Щ…ЫҢвҖҢШҜШ§ЩҶЫҢЩ… Ъ©ЩҮ Щ…ШіШ§ШӯШӘ Щ…ШіШӘШ·ЫҢЩ„ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§: Ш·ЩҲЩ„ $ \times $ Ш№ШұШ¶. ЩҫШі Ш§ЪҜШұ Щ…ШіШ§ШӯШӘ Щ…ШіШӘШ·ЫҢЩ„ ШЁШ§Щ„Ш§ ШұШ§ ШЁШ§ $S$ ЩҶШҙШ§ЩҶ ШҜЩҮЫҢЩ…ШҢ ШўЩҶЪҜШ§ЩҮ:
$$S=b \times a$$
Щ…ЫҢвҖҢШҜШ§ЩҶЫҢЩ… Ъ©ЩҮ ЪҶШұШ®Ш§ЩҶШҜЩҶ Щ…ШіШӘШ·ЫҢЩ„ ЫҢШ§ ЩҮШұ ШҙЪ©Щ„ ШҜЫҢЪҜШұЫҢШҢ ШӘШәЫҢЫҢШұЫҢ ШҜШұ Щ…ШіШ§ШӯШӘ ШўЩҶ Ш§ЫҢШ¬Ш§ШҜ ЩҶЩ…ЫҢвҖҢЪ©ЩҶШҜ. ЩҫШі Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢЩ… Щ…ШіШӘШ·ЫҢЩ„ ШЁШ§Щ„Ш§ ШұШ§ 90 ШҜШұШ¬ЩҮ ШЁЪҶШұШ®Ш§ЩҶЫҢЩ….
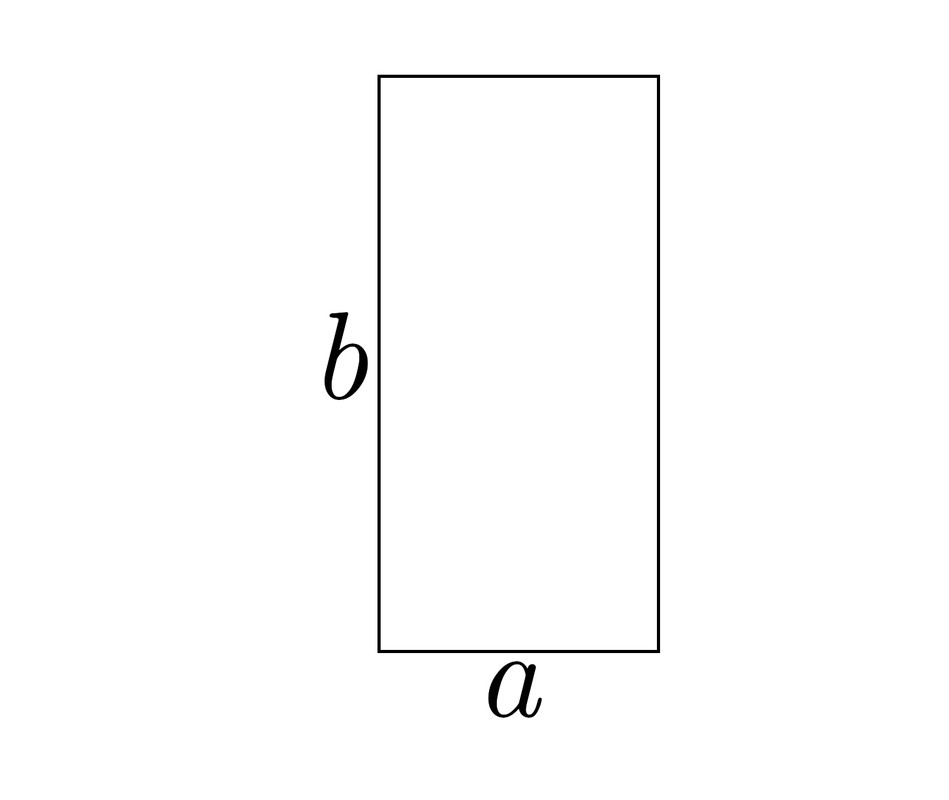
ШҜШұ Ш§ЫҢЩҶ ШөЩҲШұШӘ Щ…ШіШ§ШӯШӘ ШўЩҶ ШЁШұШ§ШЁШұ Щ…ЫҢвҖҢШҙЩҲШҜ ШЁШ§:
$$S=a \times b$$
ШҜШұ ЩҶШӘЫҢШ¬ЩҮ:
$$\left.\begin{array}{l}
S=b \times a\\ S=a \times b
\end{array}\right\rbrace\Longrightarrow a \times b=b \times a$$
ЩҫШі ШЁЩҮ ЩҮЩ…ЫҢЩҶ ШіШ§ШҜЪҜЫҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ЩҶШӘЫҢШ¬ЩҮ ЪҜШұЩҒШӘ Ъ©ЩҮ Ш№Щ…Щ„ Ш¶ШұШЁШҢ ШҜШ§ШұШ§ЫҢ Ш®Ш§ШөЫҢШӘ Ш¬Ш§ШЁЩҮвҖҢШ¬Ш§ЫҢЫҢ Ш§ШіШӘ.
Ш§Щ…Ш§ ШҜШұ Щ…ЩҲШұШҜ ШӘЩҲШ§ЩҶШҢ Щ…Ш§Ш¬ШұШ§ ШЁЩҮвҖҢЪ©Щ„ЫҢ Щ…ШӘЩҒШ§ЩҲШӘ Ш§ШіШӘ. Щ…Ш§ Ш§Ъ©ЩҶЩҲЩҶ Ш§ШІ ЫҢЪ© Ш®Ш·ШҢ ШЁЩҮ ЫҢЪ© Щ…ШұШЁШ№ ЩҲ ШЁЩҮ ЫҢЪ© Щ…Ъ©Ш№ШЁ (ЩҲ ШӯШӘЫҢ Ш§ШЁШ№Ш§ШҜ ШЁШ§Щ„Ш§ШӘШұ)ШҢ ШҜШұ ШӯШ§Щ„ ШӯШұЪ©ШӘ ЩҮШіШӘЫҢЩ…. ЩҲЩӮШӘЫҢ Ш№Щ…Щ„ЫҢШ§ШӘ ШұШ§ Щ…Ш№Ъ©ЩҲШі Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ…ШҢ Щ…Ш№ЩҶЫҢ Ъ©Ш§Щ…Щ„Ш§ЩӢ Щ…ШӘЩҒШ§ЩҲШӘЫҢ ШҜШ§ШұШҜ. Ш§ЪҜШұ ЫҢЪ© Щ…ШұШЁШ№ $3 \times 3$ ($3^2$) ШҜШ§ШҙШӘЩҮвҖҢШЁШ§ШҙЫҢЩ…ШҢ Ш§ЫҢЩҶ Щ…ШұШЁШ№ ШЁШ§ ЫҢЪ© Щ…Ъ©Ш№ШЁ $2 \times 2 \times 2$ ($2^3$) ЫҢЪ©ШіШ§ЩҶ ЩҶЫҢШіШӘ. ЫҢШ§ Щ…Ш«Щ„Ш§ЩӢ Ш§ЪҜШұ ЫҢЪ© Ш®Ш· ШЁЩҮ Ш·ЩҲЩ„ $3$ ($3^1$) ШіШ§ЩҶШӘЫҢвҖҢЩ…ШӘШұ ШҜШ§ШҙШӘЩҮвҖҢШЁШ§ШҙЫҢЩ…ШҢ ШЁШҜЫҢЩҮЫҢ Ш§ШіШӘ Ъ©ЩҮ Ш§ЫҢЩҶ Ш®Ш·ШҢ ШЁШ§ ЫҢЪ© Щ…Ъ©Ш№ШЁ $1 \times 1 \times 1$ ($1^3$) ЫҢЪ©ШіШ§ЩҶ ЩҶЫҢШіШӘ. ЩҫШі ШЁЩҮ ЩҮЩ…ЫҢЩҶ ШҜЩ„ЫҢЩ„ШҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ЪҜЩҒШӘ Ъ©ЩҮ ШӘЩҲШ§ЩҶШҢ Ш®Ш§ШөЫҢШӘ Ш¬Ш§ШЁЩҮвҖҢШ¬Ш§ЫҢЫҢ ЩҶШҜШ§ШұШҜ. ЫҢШ№ЩҶЫҢ Ш§ЪҜШұ $x,y\in\mathbb{R}$ ЩҲ $x\not = y$ШҢ ШўЩҶЪҜШ§ЩҮ Щ…Ш№Щ…ЩҲЩ„Ш§ЩӢ (ШҜШұ ШЁЫҢШҙШӘШұ Щ…ЩҲШ§ЩӮШ№) $x^y\not = y^x$.