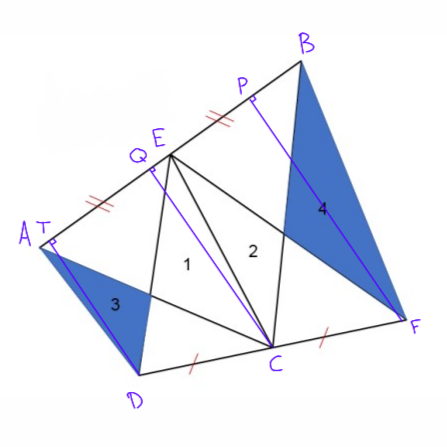
در ذوزنقه $TPFD$ چون $CQ$ با $2$ قاعده موازی است و $C$ وسط $DF$ است طبق قضیه تالس در ذوزنقه $Q$ وسط $TP$ است بنابراین طبق قضیه میان خط ( در هر ذوزنقه طول پاره خط واصل وسط دو ساق برابر با نصف مجموع دو قاعده است ) خواهیم داشت :
$ 2QC=TD+PF $
فرض میکنیم $ AE=BE=x $
خواهیم داشت :
$ S_{ABC} = \frac{2x.QC}{2} =\frac{x(TD+PF)}{2}= \frac{x.TD}{2} + \frac{x.PF}{2} =S_{ADE}+S_{BEF} $
و در آخر با حذف کردن دو مثلث مشترک در طرفین به حکم مسئله میرسیم