فرض کنید که $AB>AC$ می باشد. در شکل زیر $AM$ میانه مثلث $ABC$ می باشد. می توان نوشت: ( $\angle BAM +\angle CAM<180$)
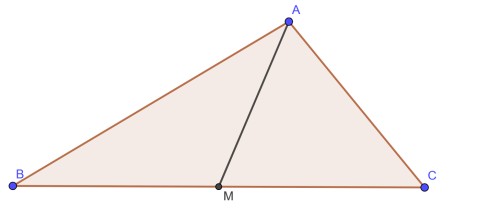
$S ABM = S AMC \Longrightarrow AB \times sin \angle BAM = AC \times sin \angle CAM \Longrightarrow sin \angle BAM < sin \angle CAM \Longrightarrow \angle BAM < \angle CAM $
اکنون از این نکته که $\angle BAM < \angle CAM $ استفاده می کنیم. توجه کنید که کمترین فاصله یک نقطه از یک خط پاره خط عمود بر آن خط از نقطه مورد نظر است. پس ارتفاع از میانه و نیمساز کوچکتر می باشد.
در شکل زیر $AD$ نیمساز زاویه $A$ می باشد.
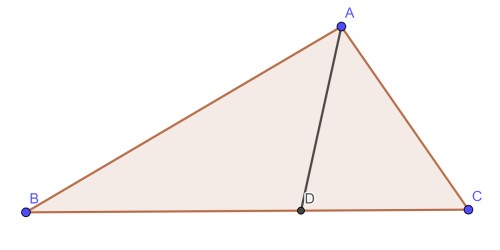
توجه کنید که $\angle BAD= \angle CAD$ که این یعنی $CD<CM$.
درشکل زیر $AH$ ارتفاع می باشد. اکنون یک نکته دیگر را یاد آور می شویم. در یک مثلث زاویه روبه رو به ضلع بزرگتر بزرگتر است از زاویه روبه رو به ضلع کوچکتر. یعنی $\angle C> \angle B$.
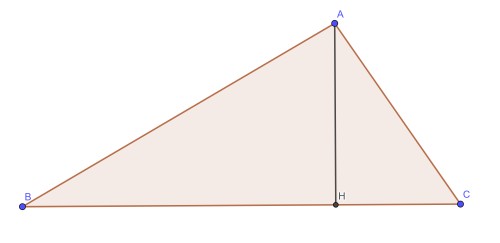
$ \angle C + \angle CAH = \angle B + \angle BAH \Longrightarrow \angle BAH > \angle CAH$
این یعنی $CH<CD$ می باشد. می توان نتیجه گرفت که:
$CH< CD< CM \Longrightarrow HD < HM \Longrightarrow HD^2 + AH^2 < HM^2 + AH^2 \Longrightarrow AD^2 < AM ^2 \Longrightarrow AD < AM $
پس نامساوی زیر برای یک مثلث مختلف اضلاع اثبات شد.
$AH < AD < AM$