با درود به همراهان گرامی. با توجه محور اعداد حقیقی و اینکه $k=\lfloor \sqrt{m} \rfloor$ است ، میدانیم $k< \sqrt{m} <(k+1)$ و $k^2<m<(k+1)^2$ . بنابراین بروی محور اعداد حقیقی داریم.
$$(1)\quad k———\sqrt{m}———(k+1)$$
$$(2)\quad k^2———m———(k+1)^2$$
از $(1)$ میتوان فهمید که اگر بتوان نسبت $\frac{\sqrt{m}-k}{(k+1)-k}$ را به $k$ افزود ، مقدار دقیق جذر را میتوان بدست آورد. ولی چون مقدار دقیق $\sqrt{m}$ در اختیار نیست ، باید این نسبت را با دقت نسبی از $(2)$ تهیه کرد. بنابراین خواهیم داشت.
$$(3)\quad \sqrt{m} \approx k+\frac{m-k^2}{(k+1)^2-k^2}$$
با ساده سازی مخرج و گرفتن مخرج مشترک در $(3)$ ، به فرمول زیر میرسیم.
$$\Longrightarrow (4)\quad \sqrt{m} \approx \frac{k(k+1)+m}{2k+1}$$
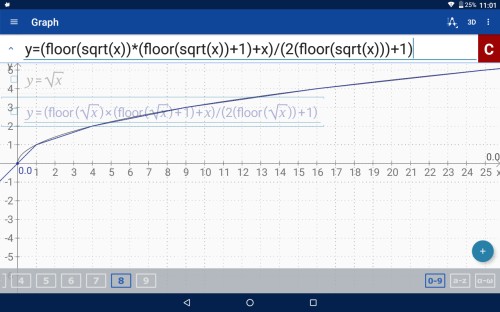
در نمودار زیر از $x$ بجای $m$ استفاده شده و مقدار واقعی جذر با مقدار بدست آمده از فرمول $(4)$ مقایسه شده. نمودار زیر که با graphing calculator تحت اندروید تهیه شده ، نشان میدهد هرچه $m$ بزرگتر باشد دقت فرمول $(4)$ بیشتر است. ضمناً بخوبی دیده میشود با دقت مناسبی که در این روش موجود است، میتوان آنرا بعنوان جواب اولیه در فرمول نیوتون استفاده کرد. ناحیه بحرانی $0$ تا $1$ در نمودار زیر نیز مشخص است که فرمول $(4)$ کمترین دقت را در این ناحیه دارد. برای ساخت این نمودار از فرمولهای زیر استفاده شده که فرمول آخر همان فرمول $(4)$ است با جایگزینی $x$ بجای $m$ .
$$y= \sqrt{x} $$
$$y=\frac{ \lfloor \sqrt{x} \rfloor×( \lfloor \sqrt{x} \rfloor +1)+x }{ 2× \lfloor \sqrt{x} \rfloor +1}$$
سرافراز و تندرست باشید.