فرض کنید $E$ و $F$ به ترتیب نقاط وسط پاره خط های $BG$ و $CG$ باشند یعنی $BE=EG$ و $CF=FG$ .
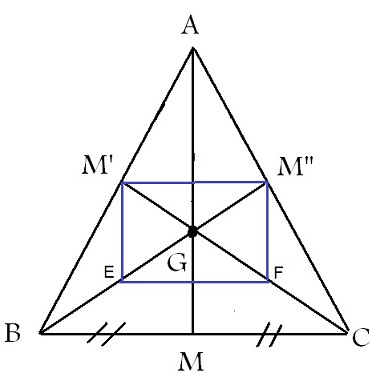
چون $M'$ و $M''$ وسط پاره خطهای $AB$ و $AC$ هستند لذا
$\frac{AM'}{M'B}=\frac{AM''}{M''B}=1$ پس بنابر عکس قضیه تالس $$M'M''\parallel BC$$
پس بنابر نتیجه قضیه تالس $\frac{AM'}{AB}=\frac{AM''}{AC}=\frac{M'M''}{BC}=\frac 12$ یعنی $$M'M''=\frac{BC}{2}$$
و با استدلال دقیقا مشابه بالا در مثلث $GBC$ داریم $$EF\parallel BC\\ EF=\frac{BC}{2}$$
بنابراین $M'M''\parallel EF , M'M''=EF$ لذا چهارضلعی $M'M''FE$ متوازی الاضلاع است. بنابراین قطرهای آن یکدیگر را نصف می کنند یعنی $EG=GM''$ و $FG=GM'$ . بنابراین
$BE=EG=GM''=\frac{BM''}{3}$ و $CF=FG=GM'=\frac{CM'}{3}$ . که این هم خواسته ی شما را نتیجه می دهد . یعنی $BG=\frac{2}{3}BM''$ و $CG=\frac23 CM'$ . برای اثبات تساوی دیگر کافی است دو میانه دیگر را در نظر گرفته و موارد بالا را تکرار کنید.