الف:چنانچه دو تابع همدیگر را قطع کنند در اینصورت مختصات محل تقاطع در هر دو تابع صدق می کند. در اینصورت برای پیدا کردن مختصات محل تلاقی معادله دو منحنی را با هم برابر قرار می دهیم.
به عنوان مثال دو تابع $f(x)=x^2$ و $g(x)=2x$ همدیگر را قطع می کنند زیرا $x^2=2x$ دارای دو جواب $x=0,x=2$ است.
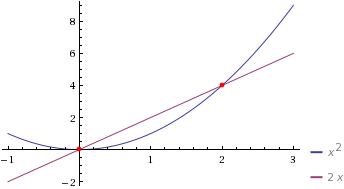
پس به طور خلاصه دو منحنی $f,g$ متقاطع اند هرگاه معادله $f(x)=g(x)$ دارای جواب باشد.
ب: یک حالت از تقاطع این است که دو منحنی بر هم مماس باشند. که در اینصورت علاوه بر اینکه معادله ی $f(x)=g(x)$ دارای جواب است مثلا فرض کنید $a$ یک جواب باشد علاوه بر این در نقطه ی تماس هر دو منحنی دارای خط مماس مشترک هستند. پس یعنی در نقطه ی $a$ شیب خط مماس بر $f$ که برابر $f'(a) $ است و شیب خط مماس بر $g$ که برابر $g'(a)$ است با هم برابر هستند یعنی $f'(a)=g'(a)$ .
پس دو منحنی $f,g$دارای مماس مشترک در نقطه $a$ هستند هرگاه:
1. $f(a)=g(a)$
2. $f'(a)=g'(a)$
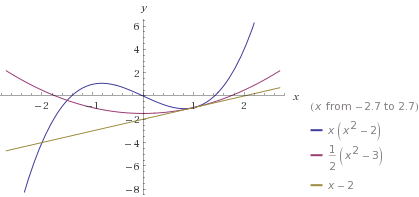
به عنوان مثال منحنی های $f(x)=x^3-2x$ و $g9x)=\frac 12x^2-\frac 32$ همدیگر را قطع می کنند زیرا $x^3-2x=\frac 12x^2-\frac 32$ دارای دو جواب $x=1,-\frac 32$ است. ولی $f'(x)=g'(x)$ یعنی $3x^2-2=x$ یا $(3x-2)(x-1)=0$ دارای دو جواب $x=1,x=-\frac 23$ است. پس نقطه ی $x=1$ نقطه ای است که شرایط مماس مشترک داشتن را دارد. لذا این دو منحنی در $x=1$ دارای مماس مشترک به معادله $y=x-2$ هستند.
ج:
بنابر آنچه در قسمت الف گفته شد دو تابع همدیگر را قطع نمی کنند اگر و تنها اگر معادله $f(x)=g(x)$ دارای جواب نباشد.
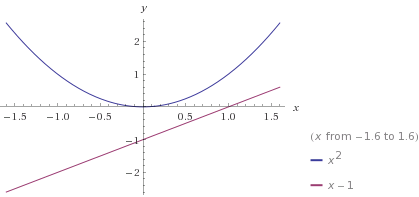
دو منحنی $f(x)=x^2$ و $g(x)=x-1$ همدیگر را قطع نمیکنند زیرا معادله $x^2=x-1$ دارای جواب نیست.(زیرا دلتای معادله درجه دوم منفی است)