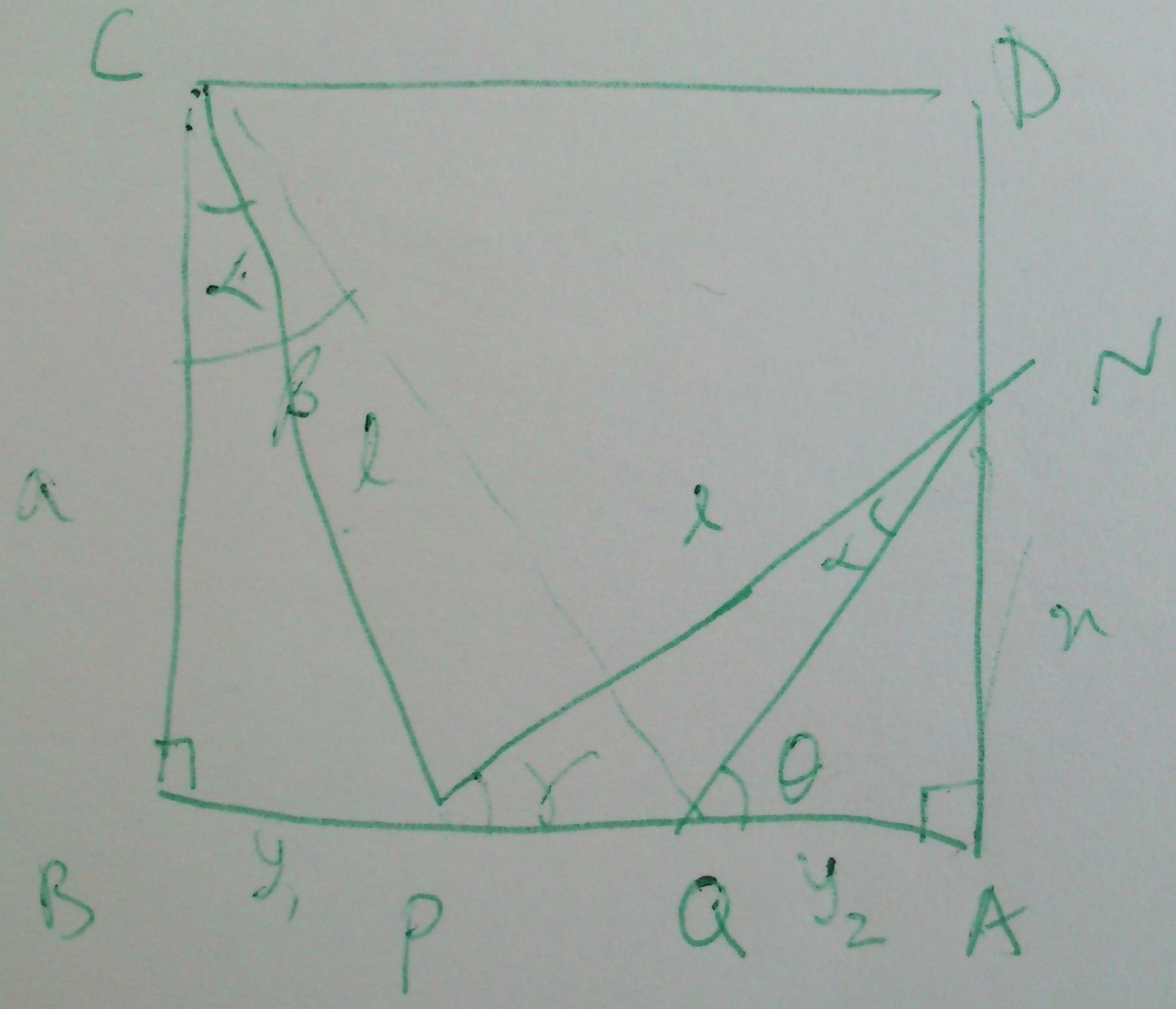
توجه کنید که شرایط گفتهشده شکل یکتایی را ایجاد نمیکنند. شما میتوانید زاویهٔ $\alpha$ را آزادانه بین صفر تا ۴۵ درجه انتخاب کنید و پس از انتخاب آن، آنگاه شکل یکتا میشود. پس حکم پرسش برای تمام حالتهای $0\leq\alpha\leq\frac{\pi}{4}$ باید ثابت شود. توجه کنید که یک آزادی دیگر و آن در انتخاب اندازهٔ یال مربع داریم ولی همانگونه که در ادامه میبینید تغییر در مقدار آن تأثیری نخواهد داشت زیرا که در محاسبات حذف میشود. در زیر تمام محاسبات سرراست هستند و از رابطههای سهگوشی (مثلثاتی) دوم دبیرستان استفاده شده است.
$$\begin{array}{l}
\tan\alpha=\frac{y_1}{a}\Longrightarrow y_1=a\tan\alpha\\
\cos\alpha=\frac{a}{\ell}\Longrightarrow \ell=a\sec\alpha\\
\overline{AP}=a-y_1\\
\gamma=arc\cos\frac{a-y_1}{\ell}=\frac{a-a\tan\alpha}{a\sec\alpha}=\\
arc\cos\dfrac{1-\frac{\sin\alpha}{\cos\alpha}}{\frac{1}{\cos\alpha}}=arc\cos(\cos\alpha-\sin\alpha)\\
x=\ell\sin\gamma=a\sec\alpha\sin(arc\cos(cos\alpha-\sin\alpha))\\
\theta=\pi-(\pi-(\alpha+\gamma))=\alpha+\gamma\\
\frac{x}{y_2}=\tan\theta\Longrightarrow y_2=x\cot\theta=\\
a\sec\alpha\sin\gamma\frac{\cos(\alpha+\gamma)}{\sin(\alpha+\gamma)}\\
\tan\beta=\dfrac{a-a\frac{\sin\gamma}{\cos\alpha}\frac{\cos(\alpha+\gamma)}{\sin(\alpha+\gamma)}}{a}=\\
\frac{\cos\alpha\sin(\alpha+\gamma)-\sin\gamma\cos(\alpha+\gamma)}{\cos\alpha\sin(\alpha+\gamma)}\\
\tan\theta=\tan(\alpha+\gamma)=\frac{\sin(\alpha+\gamma)}{\cos(\alpha+\gamma)}
\end{array}$$
اکنون با کمک رابطههای زیر
$$\begin{array}{l}
\cos(arc\cos(\cos\alpha-\sin\alpha))=\cos\alpha-\sin\alpha\\
\sin\gamma=\sqrt{1-\cos^2\gamma}\\
\tan 2\beta=\frac{2\tan\beta}{1-\tan^2\beta}
\end{array}$$
تابع زیر را به یک تابع یک متغیره با حضور فقط $\sin\alpha$ و $\cos\alpha$ تبدیل میکنیم.
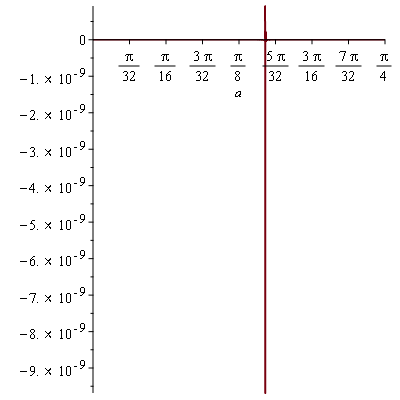
$$f(\alpha)=\tan\theta-tan 2\beta$$
با رسم عددی این تابع (که در زیر با نرمافزار Maple انجام دادیم) میبینیم که این تابع در بازهٔ خواستهشده صفر است (در نرمافزار Maple قدرمطلق حاصل عددی -تقریب- کوچکتر از $10^{-8}$ شدهاست که زمانیکه نمایش اعشاری را تا ۹ رقم اعشار گرفتهاست به نوعی صفر را میرساند.