ثابت کنید میانه وارد بر وتر نصف وتر است.

Question

ثابت کنید در مثلث قائم الزاویه ، میانه وارد بر وتر نصف وتر است؟

Comments

میانه را به اندازه خودش ادامه میدهیم بعد به دو راس مثلث وصل میكنیم(4 تا مثلث كوچیك درست میشه) بعد از راه تساوی 2 ضلع و زاویه بین 2 تا 2 تا ثابت میكنیم كه مثلث ها همنهشت اند و به این ترتیب اگه پیش برویم طبق این قضیه که اگر در مثلثی دو زاویه باهم برابر باشند آن مثلث متساوی الساقین است ثابت میشه كه میانه برابر یكی از نصفه های وتر میشود

Answer 1

اگر میانه ی $ AM$ رو به اندازه ی خودش تا نقطه ی $D$ امتداد بدیم از هم نهشتی مثلث های$AMB$ با $CMD$(بنا به حالت دو ضلع و زاویه ی بین) نتیجه میشه که اضلاع رو به رو یعنی$CD$ و$AB$ با هم برابرند،و به طور مشابه از هم نهشتی دو مثلث $AMC$و $MDB$ نتیجه میشه $AC=BD$و همچنین ما می دونیم چهارضلعی که اضلاع روبه روش باهم برابر باشه متوازی الاضلاع میشه و چون یک زاویه اش قائمه ست پس حتما شکل حاصل مستطیل خواهد بود و میدونیم در هر متوازی الاضلاع قطرها همدیگر رو نصف می کنند از طرفی میدونیم قطرهای مستطیل باهم برابرند پس محل تلاقی قطرها در مستطیل ،قطرها رو به چهار پاره خط مساوی تقسیم میکنه یعنی$AM=MD=CM=MB$ پس$AM$ نصف$CM+BM$ خواهد شد یعنی میانه ی$AM$ نصف وتر خواهد بود

Comments

ممنون از جوا ب خوب وقشنگتون اگر شکل رو هم میکشیدید بهتر میشد.(شکل رو اضافه میکنم.)
اگر وقتی عبارتی ریاضی یا حتی طول یک ضلع رو مینویسید اون رو درون دو دلار بنویسید یا بعد از کلیک روی دکمه تایپ ریاضی درون عبارت ظاهر شده بنویسید متن زیبا  تر میشود بنده این کار رو براتون در این جواب انجام میدم تفاوتش رو ببینید.

---

ممنون خیلی عالی بود

---

متشکرم. عالی بود

Answer 2

مثلث قائم الزاویه را در یک دایره محاط می‌کنیم: مرکز دایره روی وتر مثلث است پس پای میانه وارد بر وتر نیز می‌باشد از آنجایی که وتر مثلث برابر قطردایره و میانه برابر شعاع دایره است پس میانه نصف وتر است.

Answer 3

در مثلث $ AHB$ طبق رابطه فیثاغورث داریم: $$ AH^2=c^2-(x-y)^2 \tag{*}\label{*}$$ در مثلث $AHC $ طبق رابطه فیثاغورث داریم: $$ AH^2=b^2-(x+y)^2 \tag{**}\label{**}$$ و همچنین در مثلث $ AHM $ طبق رابطه فیثاغورث داریم: $$ AM^2=AH^2+y^2 $$ در رابطه آخر به جای $AH$ مساوی هایش در $\eqref{*},\eqref{**} $ را می نویسیم خواهیم داشت: $$ AM^2=c^2-(x-y)^2+y^2=c^2-x^2+2xy \tag{1}\label{1}$$ $$AM^2=b^2-(x+y)^2+y^2=b^2-x^2-2xy \tag{2}\label{2}$$ با جمع رابطه های $\eqref{1},\eqref{2} $ داریم: $$ \color{yellow}{\underline{\color{black}{2AM^2=c^2+b^2-2x^2}}} $$ و از آنجا که $ x=\frac{BC}{2}=\frac a2 $ است و $ a^2=b^2+c^2$ لذا خواهیم داشت: $$\begin{align}2AM^2&=b^2+c^2-2x^2\\&=a^2-2(\frac a2)^2\\&=a^2-\frac{a^2}{2}\\&=\frac{a^2}{2} \end{align}$$ و لذا $ AM^2=\frac{a^2}{4}$ و در نتیجه $AM=\frac{a}{2} $ .

Comments

این راه خیلی طولانیه!!
و اگر دیدگاه بالا رو نگا کنی میتونی یه راه حل راحت تر پیدا کنی.
ممنون از جوابت

---

آره .
ولی هدفم این بود : اونایی که رابطه اندازه میانه با سایر ضلع های مثلث رو  نمیدونن، ببینن.
 ایده اینم خیلی سادست (از 4تا مثلث قاءم الزاویه کمک گرفتیم) . وقتی بخوای با توضیح کامل بنویسی اینجوری طولانی میشه.
 ایده ات خیلی جالب بود. ممنون

---

ممنون جواب جالبی بود.

---

@jafar طول پاسخ مهم نیست، تنها درستی یا نادرستی پاسخ مهم است. بعلاوه هر ایده‌ای زیبایی خودش را دارد.

Answer 4

به نام خدا.

مثلث قائم الزاویه $ABC$ را در نظر بگیرید که $ \angle B=90$ می باشد.( شکل زیر)

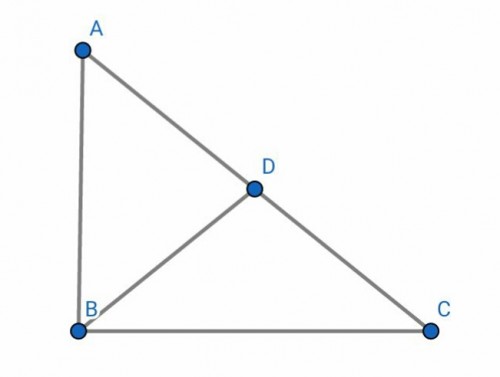
میانه $BD$ را رسم می کنیم.

فرض خلف می کنیم . فرض می کنیم که حکم نادرست است. پس دو حالت داریم:

حالت اول: $BD>AD=CD$

اگر $BD>AD$ باشد، آنگاه $ \angle A> \angle ABD$

علت هم واضح است زیرا در یک مثلث زاویه روبه رو به ضلع بزرگتر، بزرگتر است از زاویه روبه رو به ضلع کوچکتر.

چون $BD>CD$ پس $ \angle C> \angle CBD$

حال دو نامساوی فوق را جمع می کنیم:

$ \angle A+ \angle C> \angle ABD+ \angle CBD= \angle B=90$

اما این یک تناقض است! زیرا با توجه به اینکه مجموع زوایای یک مثلث $180°$ است پس باید $ \angle A+ \angle C=90$ باشد.

حالت بعدی یعنی $BD<AD=CD$ مانند قبل است و در نهایت به تناقض بر خواهیم خورد. پس فرض خلف باطل است.