Ш№Щ…Щ„ Ш¬Щ…Ш№ Ш¬Ш§ШЁШ¬Ш§ЫҢЫҢ ЩҶЫҢШіШӘШҹ ШЁЩҮ ЩҶШёШұШӘШ§ЩҶ $f_1+f_2$ ШЁШ§ $f_2+f_1$ ШӘЩҒШ§ЩҲШӘЫҢ Ш§ЫҢШ¬Ш§ШҜ Щ…ЫҢвҖҢЪ©ЩҶШҜШҹ ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ Ш§ЫҢЩҶЪ©ЩҮ ШҜШұ ЫҢЪ©ЫҢ ШӘШ§ШЁШ№ ЫҢЪ©ЩҸЩ… ШұШ§ ЩҶЫҢЩ…вҖҢЩҫЫҢЩҲШіШӘЩҮЩ” ШЁШ§Щ„Ш§ЫҢЫҢ ЪҜШұЩҒШӘЩҮвҖҢШ§ЫҢШҜ ЩҲ ШҜЩҲЩ…ЫҢ ШұШ§ ЩҫШ§ШҰЫҢЩҶЫҢ ШӘЩҒШ§ЩҲШӘЫҢ ШЁШ§ ШҜЩҲЩ…ЫҢ Ъ©ЩҮ ШӘШ§ШЁШ№ ЫҢЪ©ЩҸЩ… ШұШ§ ЩҫШ§ШҰЫҢЩҶЫҢ ЩҲ ШӘШ§ШЁШ№ ШҜЩҲЩ… ШұШ§ ШЁШ§Щ„Ш§ЫҢЫҢ ЪҜШұЩҒШӘЫҢШҜ ЩҶШҜШ§ШұШҜ. ЩҲ ШҜШұ Ш§ЫҢЩҶШөЩҲШұШӘ Ш§ЪҜШұ Ш§ШҜШ№Ш§ЫҢШӘШ§ЩҶ ШҜШұШіШӘ ШЁШ§ШҙШҜ ЪҶШұШ§ ЫҢЪ© Ш¶ШұШЁ ЩҶЩ…ЫҢвҖҢЪҜЩҲШҰЫҢШҜ Ш¬Щ…Ш№ ШҜЩҲ ШӘШ§ШЁШ№ Ъ©ЩҮ ЫҢЪ©ЫҢ ЩҶЫҢЩ…вҖҢЩҫЫҢЩҲШіШӘЩҮЩ” ШЁШ§Щ„Ш§ЫҢЫҢ ЩҲ ШҜЫҢЪҜШұЫҢ ЩҫШ§ШҰЫҢЩҶЫҢ ШЁШ§ШҙШҜШҢ ШӘШ§ШЁШ№ЫҢ ЩҫЫҢЩҲШіШӘЩҮ (Щ…Ш№Щ…ЩҲЩ„ЫҢ) Щ…ЫҢвҖҢШҙЩҲШҜШҹ
ШЁШұЪҜШұШҜЫҢЩ… ШЁЩҮ ЩҫШұШіШҙ.
ШӘШ№ШұЫҢЩҒ ЩҶЫҢЩ…вҖҢЩҫЫҢЩҲШіШӘЩҮЩ” ШЁШ§Щ„Ш§ЫҢЫҢ ЩҲ ЩҶЫҢЩ…вҖҢЩҫЫҢЩҲШіШӘЩҮЩ” ЩҫШ§ШҰЫҢЩҶЫҢ ШұШ§ ЫҢШ§ШҜШўЩҲШұЫҢ Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ…. ЫҢЪ© ШӘШ§ШЁШ№ $f\colon\mathbb{R}\to\mathbb{R}$ ШұШ§ ЩҶЫҢЩ…вҖҢЩҫЫҢЩҲШіШӘЩҮЩ” ШЁШ§Щ„Ш§ЫҢЫҢ ЪҜЩҲШҰЫҢЩ… ЩҮШұ ЪҜШ§ЩҮ ШЁШұШ§ЫҢ ЩҮШұ ЩҶЩӮШ·ЩҮЩ” $x_0\in\mathbb{R}$ ШҜШ§ШҙШӘЩҮвҖҢШЁШ§ШҙЫҢЩ… $f(x_0)\geq\limsup_{x\to x_0}f(X)$. ЫҢШ№ЩҶЫҢ ШҜШұ ЩҮШұ ЩҶЩӮШ·ЩҮвҖҢШ§ЫҢШҢ Щ…ЩӮШҜШ§Шұ ШӘШ§ШЁШ№ ШЁШ§ЫҢШҜ Ш§ШІ ШЁШІШұЪҜШӘШұЫҢЩҶ ШӯШҜ ШҜЩҶШЁШ§Щ„ЩҮвҖҢЩҮШ§ЫҢ $\lbrace f(x_i)\rbrace_{i=1}^\infty$Ш§ЫҢ Ъ©ЩҮ $\lbrace x_i\rbrace_{i=1}^\infty$ЩҮШ§ ШЁЩҮ $x_0$ Щ…ЫҢЩ„ Щ…ЫҢвҖҢЪ©ЩҶЩҶШҜ ШЁШІШұЪҜШӘШұ ЫҢШ§ Щ…ШіШ§ЩҲЫҢ ШЁШ§ШҙШҜ. Ш®ЫҢЩ„ЫҢ ШіШ§ШҜЩҮ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢШҜ ШЁШЁЫҢЩҶЫҢШҜ Ъ©ЩҮ ЫҢЪ© ШӘШ§ШЁШ№ ЩҫЫҢЩҲШіШӘЩҮШҢ ЩҶЫҢЩ…вҖҢЩҫЫҢЩҲШіШӘЩҮЩ” ШЁШ§Щ„Ш§ЫҢЫҢ ЩҶЫҢШІ Ш§ШіШӘ. ЪҶШұШ§Шҹ ЪҶЩҲЩҶ ШЁШұШ§ЫҢ ЩҮШұ ШҜЩҶШЁШ§Щ„ЩҮЩ” $\lbrace x_n\rbrace\to x_0$ ШҜШ§ШұЫҢЩ… $\lbrace f(x_n)\rbrace\to f(x_0)$ ЩҫШі Щ…Ш¬Щ…ЩҲШ№ЩҮЩ” ШӯШҜЩҮШ§ЫҢЫҢ Ъ©ЩҮ ШЁШ§ЫҢШҜ Ш§ШІ ШўЩҶ ШЁЫҢШҙЫҢЩҶЩҮ ШЁЪҜЫҢШұЫҢЩ… ШӘЪ©вҖҢШ№Ш¶ЩҲЫҢ Ш§ШіШӘ ЩҫШі $\limsup_{x\to x_0}f(x)$ ШЁШұШ§ШЁШұ ШЁШ§ $f(x_0)$ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ ШҙШұШ· ШЁШІШұЪҜШӘШұЫҢШ§Щ…ШіШ§ЩҲЫҢ ШөШҜЩӮ Щ…ЫҢвҖҢЪ©ЩҶШҜ. Ш§Ъ©ЩҶЩҲЩҶ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ШӘЩ…ШұЫҢЩҶ ШіШ§ШҜЩҮ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢШҜ ЩҶШҙШ§ЩҶ ШҜЩҮЫҢШҜ Ъ©ЩҮ Ш§ЪҜШұ ЫҢЪ© ШӘШ§ШЁШ№ Ш§ЩҒШІШ§ЫҢШҙЫҢ (ЩҶЩҮ Ш§Щ„ШІШ§Щ…Ш§ Ш§Ъ©ЫҢШҜ) ШҜШ§ШҙШӘЩҮвҖҢШЁШ§ШҙЫҢЩ…ШҢ ШўЩҶЪҜШ§ЩҮВ ЩҶЫҢЩ…вҖҢЩҫЫҢЩҲШіШӘЩҮЩ” ШЁШ§Щ„Ш§ЫҢЫҢ Ш§ШіШӘ Ш§ЪҜШұ ЩҲ ШӘЩҶЩҮШ§ Ш§ЪҜШұ ШҜШұ ЩҶЩӮШ·ЩҮвҖҢЩҮШ§ЫҢ ЩҶШ§ЩҫЫҢЩҲШіШӘЪҜЫҢвҖҢШ§Шҙ Щ…ЩӮШҜШ§ШұШҙ ШЁШұШ§ШЁШұ ШЁШ§ ШӯШҜ ШұШ§ШіШӘШҙ ШЁШ§ШҙШҜ.
ШЁЩҮ ШұЩҲШҙ ЫҢЪ©ШіШ§ЩҶ ЩҶЫҢШІ ЩҶЫҢЩ…вҖҢЩҫЫҢЩҲШіШӘЩҮЩ” ЩҫШ§ШҰЫҢЩҶЫҢ ШӘШ№ШұЫҢЩҒ Щ…ЫҢвҖҢШҙЩҲШҜ ЩҲ ЩҶЪ©ШӘЩҮвҖҢЩҮШ§ЫҢ ЫҢЪ©ШіШ§ЩҶЫҢ ШұШ§ ШҜШ§ШұЫҢЩ…. ШЁШұШ§ЫҢ ЩҶЩ…ЩҲЩҶЩҮШҢ ЫҢЪ© ШӘШ§ШЁШ№ Ш§ЩҒШІШ§ЫҢШҙЫҢШҢ ЩҶЫҢЩ…вҖҢЩҫЫҢЩҲШіШӘЩҮЩ” ЩҫШ§ШҰЫҢЩҶЫҢ Ш§ШіШӘ Ш§ЪҜШұ ЩҲ ШӘЩҶЩҮШ§ Ш§ЪҜШұ ШҜШұ ЩҶЩӮШ·ЩҮвҖҢЩҮШ§ЫҢ ЩҶШ§ЩҫЫҢЩҲШіШӘЪҜЫҢвҖҢШ§ШҙШҢ Щ…ЩӮШҜШ§ШұШҙ ШЁШұШ§ШЁШұ ШЁШ§ ШӯШҜ ЪҶЩҫШҙ ШЁШ§ШҙШҜ.
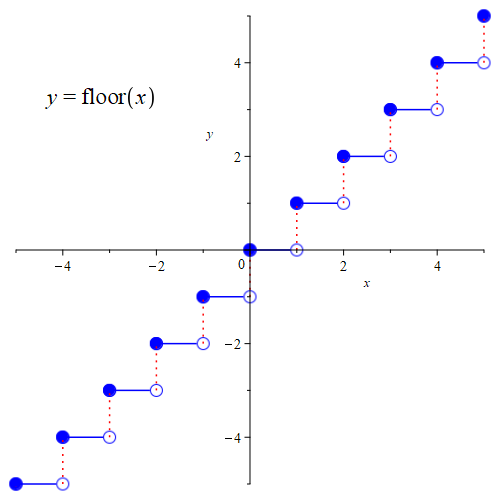
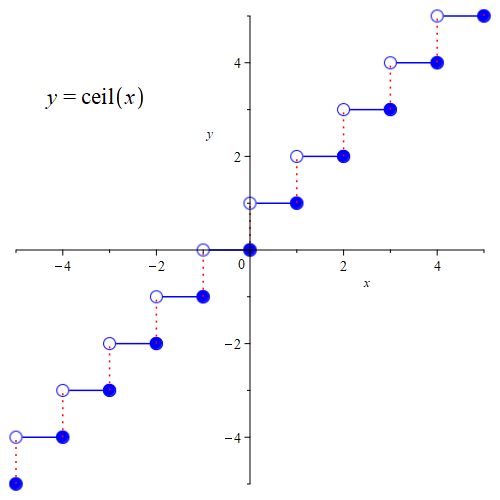
ЩҫШі Ш®ЫҢЩ„ЫҢ ШұШ§ШӯШӘ ШӘШ§ШЁШ№ Ш¬ШІШЎ ШөШӯЫҢШӯ Ъ©ЩҮ Ш§ЩҒШІШ§ЫҢШҙЫҢ (ЩҶШ§Ш§Ъ©ЫҢШҜ) ЩҲ ЩҫЫҢЩҲШіШӘЩҮ Ш§ШІ ШіЩ…ШӘ ШұШ§ШіШӘШҢ ШҜШұ ЩҶШӘЫҢШ¬ЩҮ ЩҶЫҢЩ…вҖҢЩҫЫҢЩҲШіШӘЩҮЩ” ШЁШ§Щ„Ш§ЫҢЫҢ Ш§ШіШӘ ЩҲ ШӘШ§ШЁШ№ ШіЩӮЩҒ (Щ…Ш§ЩҶЩҶШҜ Ш¬ШІШЎШөШӯЫҢШӯ Ш§ШіШӘ ШЁШ§ Ш§ЫҢЩҶ ШӘЩҒШ§ЩҲШӘ Ъ©ЩҮ Ш№ШҜШҜЩҮШ§ЫҢ ЩҶШ§ШөШӯЫҢШӯ ШұШ§ ШЁЩҮ ШіЩ…ШӘ ШЁШ§Щ„Ш§ ЪҜШұШҜ Щ…ЫҢвҖҢЪ©ЩҶШҜ ЩҫШі ШіЩӮЩҒЩҗ $3.14$ Щ…ЫҢвҖҢШҙЩҲШҜ Ыҙ ЩҶЩҮ Ыі) Ъ©ЩҮ Ш§ЩҒШІШ§ЫҢШҙЫҢ (ЩҶШ§Ш§Ъ©ЫҢШҜ) ЩҲ ЩҫЫҢЩҲШіШӘЩҮ Ш§ШІ ШіЩ…ШӘ ЪҶЩҫШҢ ШҜШұ ЩҶШӘЫҢШ¬ЩҮ ЩҶЫҢЩ…вҖҢЩҫЫҢЩҲШіШӘЩҮЩ” ЩҫШ§ШҰЫҢЩҶЫҢ Ш§ШіШӘ ШұШ§ ШҜШұ ЩҶШёШұ ШЁЪҜЫҢШұЫҢШҜ. ШҜШұ ШІЫҢШұ ЩҶЩ…ЩҲШҜШ§Шұ Ш§ЫҢЩҶ ШҜЩҲ ШӘШ§ШЁШ№ ШұШіЩ… ШҙШҜЩҮвҖҢШ§ЩҶШҜ. ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ШҜШұ Ш§ЩҶЪҜЩ„ЫҢШіЫҢ floor ЩҲ ceiling ШЁЩҮ ШӘШұШӘЫҢШЁ ШЁЩҮ Щ…Ш№ЩҶШ§ЫҢ Ъ©ЩҒ ЩҲ ШіЩӮЩҒ ЩҮШіШӘЩҶШҜ Ъ©ЩҮ ШЁШұШ§ЫҢ ЩҮЩ…ЫҢЩҶ ЩҶЫҢШІ ШЁШұШ®ЫҢ ШӘШ§ШЁШ№ Ш¬ШІШЎШөШӯЫҢШӯ ЩҲ ШіЩӮЩҒ ШұШ§ ШЁШ§ floor ЩҲ ceil ЩҶЩ…Ш§ЫҢШҙ Щ…ЫҢвҖҢШҜЩҮЩҶШҜ. ШҜШіШӘЩҲШұЩҮШ§ЫҢ ШұШіЩ… Ш§ЫҢЩҶ ЩҶЩ…ЩҲШҜШ§ШұЩҮШ§ ШЁШ§ ЩҶШұЩ…вҖҢШ§ЩҒШІШ§Шұ Maple ЩҶЫҢШІ ЪҜШ°Ш§ШҙШӘЩҮвҖҢШҙШҜЩҮвҖҢШ§ЩҶШҜ.
floorLineSegments:=[seq(plot([[i,i],[i+1,i]],'color'='blue'),i=-5..5)]:
floorFilledPoints:=plots:-pointplot([seq([i,i],i=-5..5)],'symbol'='solidcircle','symbolsize'=20,'color'='blue'):
floorEmptyPoints:=plots:-pointplot([seq([i+1,i],i=-5..5)],'symbol'='solidcircle','symbolsize'=20,'color'='white'):
floorPointsBorders:=plots:-pointplot([seq([i,i],i=-5..5),seq([i+1,i],i=-5..5)],'symbol'='circle','symbolsize'=20,'color'='blue'):
floorDottedLines:=[seq(plots:-display(plottools:-line([i,i-1],[i,i],'linestyle'='dot','color'='red')),i=-5..5)]:
floorText:=plots:-textplot([-4.5,3,'typeset'(y=floor(x))],'font'=['times',18],'color'='black','align'={'above','right'}):
plots:-display(seq(floorLineSegments[i],i=1..numelems(floorLineSegments)),floorFilledPoints,floorEmptyPoints,floorPointsBorders,seq(floorDottedLines[i],i=1..numelems(floorDottedLines)),floorText,'view'=[-5..5,-5..5],'labels'=[x,y]);
ceilLineSegments:=[seq(plot([[i,i+1],[i+1,i+1]],'color'='blue'),i=-5..5)]:
ceilFilledPoints:=plots:-pointplot([seq([i,i],i=-5..5)],'symbol'='solidcircle','symbolsize'=20,'color'='blue'):
ceilEmptyPoints:=plots:-pointplot([seq([i,i+1],i=-5..5)],'symbol'='solidcircle','symbolsize'=20,'color'='white'):
ceilPointsBorders:=plots:-pointplot([seq([i,i],i=-5..5),seq([i,i+1],i=-5..5)],'symbol'='circle','symbolsize'=20,'color'='blue'):
ceilDottedLines:=[seq(plots:-display(plottools:-line([i,i],[i,i+1],'linestyle'='dot','color'='red')),i=-5..5)]:
ceilText:=plots:-textplot([-4.5,3,'typeset'(y=ceil(x))],'font'=['times',18],'color'='black','align'={'above','right'}):
plots:-display(seq(ceilLineSegments[i],i=1..numelems(ceilLineSegments)),ceilFilledPoints,ceilEmptyPoints,ceilPointsBorders,seq(ceilDottedLines[i],i=1..numelems(ceilDottedLines)),ceilText,'view'=[-5..5,-5..5],'labels'=[x,y]);
ЩҲ Ш§Щ…Ш§ Ш§Ъ©ЩҶЩҲЩҶ Ш¬Щ…Ш№ Ш§ЫҢЩҶ ШҜЩҲ ШӘШ§ШЁШ№ ШұШ§ ШҜШұ ЩҶШёШұ ШЁЪҜЫҢШұЫҢШҜ. ЩҶЩ…ЩҲШҜШ§Шұ ШўЩҶ ШұШ§ ШҜШұ ШІЫҢШұ Щ…ЫҢвҖҢШЁЫҢЩҶЫҢШҜ.
sumLineSegments:=[seq(plot([[i,2*i+1],[i+1,2*i+1]],'color'='blue'),i=-5..5)]:
sumFilledPoints:=plots:-pointplot([seq([i,2*i],i=-5..5)],'symbol'='solidcircle','symbolsize'=20,'color'='blue'):
sumEmptyPoints:=plots:-pointplot([seq([i,2*i+1],i=-5..5),seq([i,2*i-1],i=-5..5)],'symbol'='solidcircle','symbolsize'=20,'color'='white'):
sumPointsBorders:=plots:-pointplot([seq([i,2*i],i=-5..5),seq([i,2*i+1],i=-5..5),seq([i,2*i-1],i=-5..5)],'symbol'='circle','symbolsize'=20,'color'='blue'):
sumDottedLines:=[seq(plots:-display(plottools:-line([i,2*i-1],[i,2*i+1],'linestyle'='dot','color'='red')),i=-5..5)]:
sumText:=plots:-textplot([-4.5,3,'typeset'(y=floor(x)+ceil(x))],'font'=['times',18],'color'='black','align'={'above','right'}):
plots:-display(seq(sumLineSegments[i],i=1..numelems(sumLineSegments)),sumFilledPoints,sumEmptyPoints,sumPointsBorders,seq(sumDottedLines[i],i=1..numelems(sumDottedLines)),sumText,'view'=[-5..5,-5..5],'labels'=[x,y]);
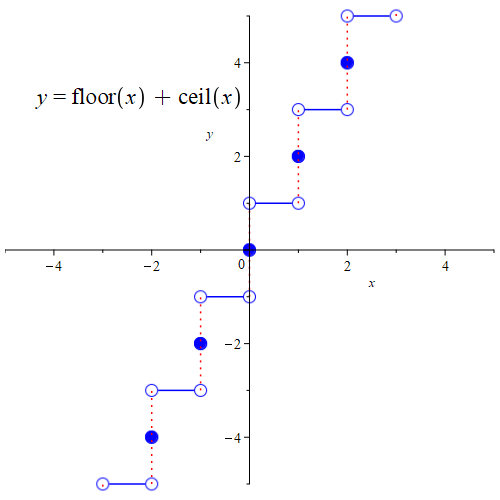
ЩҮЩ…Ш§ЩҶвҖҢЪҜЩҲЩҶЩҮ Ъ©ЩҮ Щ…ЫҢвҖҢШЁЫҢЩҶЫҢШҜ ЫҢЪ© ШӘШ§ШЁШ№ Ш§ЩҒШІШ§ЫҢШҙЫҢ (ЩҶШ§Ш§Ъ©ЫҢШҜ) Ш§ШіШӘ Ъ©ЩҮ ШҜШұ ЩҶЩӮШ·ЩҮвҖҢЩҮШ§ЫҢ ШөШӯЫҢШӯ Ш§ШІ ЩҮЫҢЪҶ ШіЩ…ШӘЫҢ ЩҫЫҢЩҲШіШӘЩҮ ЩҶЫҢШіШӘ. ШҜШұ ЩҶШӘЫҢШ¬ЩҮ ЩҶЩҮ ЩҶЫҢЩ…вҖҢЩҫЫҢЩҲШіШӘЩҮЩ” ШЁШ§Щ„Ш§ЫҢЫҢ Ш§ШіШӘ ЩҲ ЩҶЩҮ ЩҶЫҢЩ…вҖҢЩҫЫҢЩҲШіШӘЩҮЩ” ЩҫШ§ШҰЫҢЩҶЫҢ. ЩҫШі ЩҮШұ ШҜЩҲ Ш§ШҜШ№Ш§ЫҢШӘШ§ЩҶ ШұШҜ Щ…ЫҢвҖҢШҙЩҲЩҶШҜ.