میدانیم :
$$projdim=max\{ i: \beta _{i,j} \neq 0 \ \ for \ some \ j \}$$
و
$$reg=max\{ j: \beta _{i,i+j} \neq 0 \ \ for \ some \ i \}$$
در $Resolution $ مقدار $ i $ از $0 $ شروع شده و بیشترین آن برابر $ projdim$ است و طبق فرمول بالا در بین $ \beta _{i,i+j} \neq 0$ بیشترین مقدار $j$برابر
$reg $ است فرض برای $ x_{i0} $ داشته باشیم $ \beta _{i0,i0+reg} \neq 0$
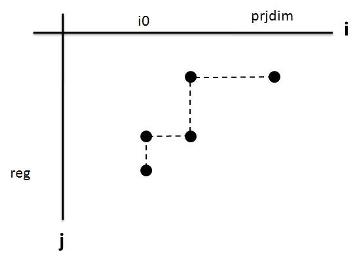
برای رسم $\beta$دیاگرام یک محور را برای مقادیر $i$ و محور عمودی را برابر مقادیر $j$ میگیریم و اگر $ \beta _{i,i+j} \neq 0$ باشد آن را در نقطه ای به مختصات $ (i,j) $ نمایش میدهیم
چون هدف از این نمودار پیدا کردن نقاط $Extremal$ است و تمام نقاطی که مقدار $ i $ آنها از $ i0 $ کمتر است نمیتوانند اکسترمال باشد نقطه ی شروع رسم نمودار نقطه ی $(i0,reg)$ است. و نقاط دیگر را هم مشخص میکنیم و با خط چین آنها را بهم وصل میکنیم.
( در $Resolution $ ممکن است در یک مرحله یعنی برای یک $i$ ثابت چند $j$ داشته باشیم در این حالت خط چین روبه بالا و عمود است)
مثال:
برای $ \alpha $ دیاگرام با توجه به گزاره ی $4.3.4$ برای هر $ i < depth $ داریم $\alpha _{ij} =0$
لذا نمودار را باید از $ i=depth $ شروع شود و با توجه به تعریف $Extremal$ تا نقطه ی $ (i0,reg) $ ادامه دارد(در واقع برای $ $ هیچ کدام از نقاط نمیتوانند $Extremal$ باشند لذا از کشیدن آنها صرف نظر می شود) و مشابه $\beta$دیاگرام، رسم می شود.
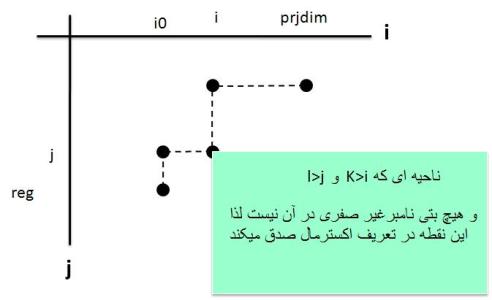
تعریف اکسترمال بودن یک بتی نامبر:
$ \beta _{i,i+j} \neq 0$ را اکسترمال می گوییم هرگاه برای هر $(k,l) \neq (i,j)$ که $k \geq i,l \geq j $ داشته باشیم $\beta _{k,k+l} =0 $
با توجه به شکل زیر هر نقطه از این نوع که گوشه است یک نقطه ی اکسترمال است(اکسترمال =گوشه ای) لذا اگر $\beta$ دیاگرام رسم شده باشد گوشه های خارجی نقاط اکسترمال هستند.