اگر به تلاش خودتان اشاره میکردید همان دو ماه پیش راهنمایی مناسب میگرفتید. عدد مختلط $z$ را $x+iy$ بگیرید که هنوز مقدارهای $x$ و $y$ را نمیدانیم. دو عدد دیگر یکی $i=0+1i$ و دیگری
$$iz=i(x+iy)=-y+ix$$
هستند. این سه عدد متناظر با سه نقطه در صفحهٔ $x\circ y$ هستند. نقطههای متناظر با $i$ و $z$ و $iz$ را به ترتیب نامهای $A$ و $B$ و $C$ بدهید. درازای هر یال از سهگوشِ $ABC$ را در زیر مییابیم.
\begin{align}
|AB| &= |B-A|=|(x+iy)-(i)|=|x+(y-1)i|=\sqrt{x^2+(y-1)^2}\\
|AC| &= |C-A|=|(-y+xi)-(i)|=|-y+(x-1)i|=\sqrt{y^2+(x-1)^2}\\
|BC| &= |C-B|=|(-y-x)+(x-y)i|=\sqrt{(x+y)^2+(x-y)^2}
\end{align}
برای اینکه این سهگوش دارای یالهای با درازای یکسان باشد باید دستگاه دوبرابری-دومجهولیِ $|AB|=|AC|$ و $|AB|=|BC|$ را حل کنیم. برابریِ یکُم به ما نتیجهٔ زیر را میدهد.
\begin{align}
|AB|=|AC| &\Longleftrightarrow x^2+y^2-2y+1=y^2+x^2-2x+1\\
&\Longleftrightarrow -2y=-2x\\
&\Longleftrightarrow y=x
\end{align}
اکنون این نتیجه را در برابریِ دوم جایگذاری میکنیم.
\begin{align}
|AC|=|BC| &\Longleftrightarrow x^2+y^2-2y+1=2x^2+2y^2\\
&\overset{y=x}{\Longleftrightarrow} 2x^2+2x-1=0
\end{align}
از حل این برابری درجهٔ دوی یکمتغیره داریم $x=\frac{-1\pm\sqrt{3}}{2}$. پس گزینش برای $z$ که سهگوش با ویژگیِ خواستهشده را ایجاد کند ممکن است. در هر مورد درازای یالهای سهگوش برابر با $|BC|$ که میشود $\sqrt{2x^2+2x^2}=2|x|$ است میشود، به یاد آورید که بخش حقیقی و موهومیِ $z$ با هم برابر شدند (نتیجهٔ برابریِ یکُم در بالا). یعنی اگر با دو رقم پس از اعشار بخواهید یک سهگوش با درازای یالهای برابر با $0.73$ و برای دیگری $2.73$ داریم. شکل این دو سهگوش در زیر آوردهشدهاست (کشیدهشده با نرمافزار Maple میپل).
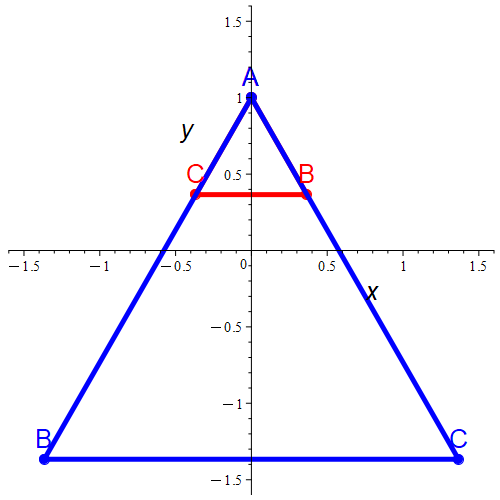
سهگوش دوم با رنگ آبی و سهگوش یکُم با گوشههای $A$ آبی و $B$ و $C$ -ِ قرمز مشخص شدهاند.