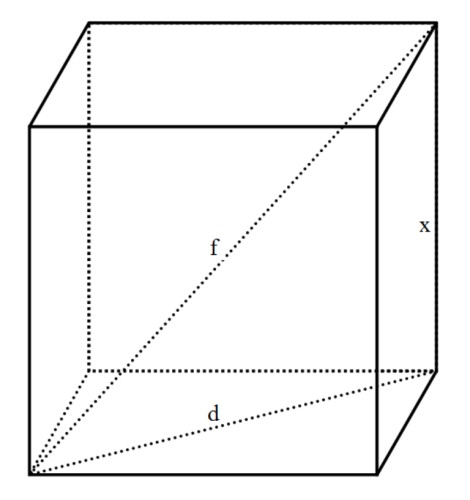
به مکعب فوق دقت کنید. بزرگترین طول در مکعب همان قطر داخلی آن یعنی $f$ است و قطر کره باید مساوی $f$ باشد تا مکعب را دربر گیرد.
$x=$ طول هریک از اضلاع مکعب
$d=$ قطر هریک از سطوح مکعب
$f=$ قطر داخلی مکعب = قطر کره
$s=6x^2$ = سطح کل مکعب
طبق این فرضیات با قضیه فیثاغورث داریم.
$$d= \sqrt{x^2+x^2}= \sqrt{2} x$$
$$f=\sqrt{d^2+x^2}= \sqrt{ \left( \sqrt{2}x\right)^2+x^2 }= \sqrt{3}x $$
$$ \Longrightarrow \frac{3}{4} =\sqrt{3}x \Longrightarrow x= \frac{3}{4 \sqrt{3} } = \frac{ \sqrt{3} }{4} $$
$$s=6x^2=6× \left(\frac{ \sqrt{3} }{4}\right)^2=6× \frac{3}{16}= \frac{9}{8} =1.125 $$