هر خط با نوشتن معادله اش مشخص می شود. برای نوشتن معادله هر خطی یک نقطه و شیب آن لازم است.
برای نوشتن معادله ی خط مماس بر منحنی تابع $y=f(x)$ در نقطه $(a,f(a))$ چون خط مماس از این نقطه عبور می کند پس کافی است شیب خط مماس را به دست آوریم.
برای این کار یک نقطه در نزدیکی نقطه $(a,f(a))$ مثل $(a+h,f(a+h))$ در نظر میگیریم. در اینصورت شیب خطی که از این دو نقطه می گذرد برابر است با:
$$\frac{f(a+h)-f(a)}{a+h-a}=\frac{f(a+h)-f(a)}{h}$$
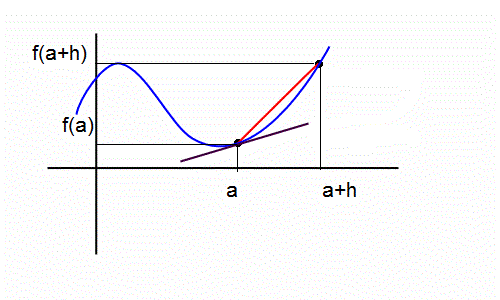
ولی این شیب برابر شیب خط مماس نیست. برای به دست آوردن شیب خط مماس باید نقطه ای که در نزدیکی $(a,f(a))$ در نظر میگیریم بسیار به سمت این نقطه نزدیک کنیم. اما نزدیک کردن در ریاضیات یعنی حد یعنی $(a+h,f(a+h))$ که به اندازه $h$ از $a$ جلوتر رفته ایم و انتخاب کرده ایم این فاصله $h$ را بسیار کم کنیم یعنی $h$ را به سمت صفر میل دهیم:
$$m=\lim_{h\to 0}\frac{f(a+h)-f(a)}h$$
که شیب خط مماس است. و در ریاضیات به حد بالا مشتق تابع $f$ در نقطه $a$ می گوییم. در اینصورت معادله خط مماس برابر است با:
$$y-f(a)=m(x-a)$$