متوجهِ «آیا» نمیشوم! دستگاه مختصات برای آدرسدهی نقاط به کار میرود و صد البته اگر دو دستگاهِ مختصات برای یک فضا داشتهباشید هر کاری که در یکی بتوان انجام داد در دیگری نیز میتوانید انجام بدهید.
همانگونه که برای مساحت و یا حجم در دستگاههای قطبی یا کروی ابتدا اِلمانِ مساحت و حجم را پیدا میکردید (حتی در دستگاه کارتزی نیز باید این کار را بکنید که چون پیشفرض آشنا هستید نیازی به انجام نمیداشتید) و سپس ناحیه را با بازهها و تابع در دستگاه مختصات بیان و در آخر انتگرال میگرفتید. معمولا المان مساحت و حجم در کارتزی را برمیداشتید و با دترمینان ماتریس ژاکوبی و تبدیل مختصات المان مساحت و حجم را در دستگاههای دیگر محاسبه میکردید (این تنها راه ممکن نیست بلکه روشی است که برایتان سادهتر و سریعتر بود).
مختصات کارتزی در دستگاه استوانهای به شکلِ
$$x=r\cos\theta,\quad y=r\sin\theta,\quad z=z$$
بیان میشوند پس دترمینان ماتریس ژآکوبی این تبدیل مختصات برابر میشود با:
$$\det\frac{\partial (x,y,z)}{\partial (r,\theta,z)}=\begin{vmatrix} \cos\theta & -r\sin\theta & 0\\ \sin\theta & r\cos\theta & 0\\ 0 & 0 & 1\end{vmatrix}=r$$
اکنون ناحیهٔ یک کره در مختصات قطبی را باید بیان کنیم. شکل زیر را ببینید.
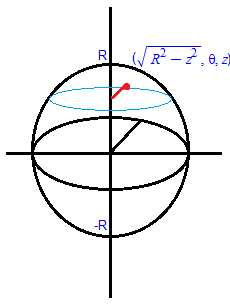
$z$ها از $-R$ تا $R$ تغییر میکنند. سپس برای یک $z$ در این ناحیه، $\theta$ از $0$ تا $2\pi$ تغییر میکند. سپس برای یک $z$ و $\theta$، $r$ از $0$ تا $\sqrt{R^2-z^2}$ تغییر میکند. پس انتگرال سهگانهٔ حجم کره در این دستگاه برابر میشود با:
$$\int_{-R}^R\int_0^{2\pi}\int_{0}^{\sqrt{R^2-z^2}}rdrd\theta dz$$
که برابر با $\frac{4}{3}\pi R^3$ است.